卷积神经网络

在之前的文章里,对28 X 28的图像,我们是通过把它展开为长度为784的一维向量,然后送进全连接层,训练出一个分类模型.这样做主要有两个问题

1. 图像在同一列邻近的像素在这个向量中可能相距较远。它们构成的模式可能难以被模型识别。
2. 对于大尺寸的输入图像，使用全连接层容易造成模型过大。假设输入是高和宽均为1000像素的彩色照片（含3个通道）。即使全连接层输出个数仍是256，该层权重参数的形状是\(3,000,000\times 256\),按照参数为float,占用4字节计算,它占用了大约3000000 X 256 X4bytes=3000000kb=3000M=3G的内存或显存。

很显然,通过使用卷积操作可以有效的改善这两个问题.关于卷积操作,池化操作等,参见置顶文章https://www.cnblogs.com/sdu20112013/p/10149529.html．

LENET

lenet是比较早期提出来的一个神经网络,其结构如下图所示.
　

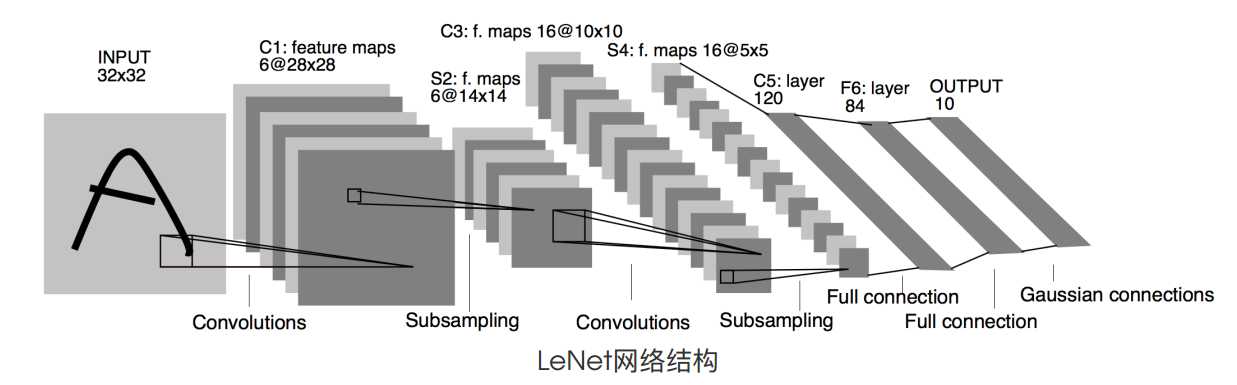
LeNet的结构比较简单,就是2次重复的卷积激活池化后面接三个全连接层.卷积层的卷积核用的5 X 5,池化用的窗口大小为2 X 2,步幅为2．
对我们的输入(28 x 28)来说,卷积层得到的输出shape为[batch,16,4,4],在送入全连接层前,要reshape成[batch,16x4x4].可以理解为通过卷积,对没一个样本,我们
都提取出来了16x4x4=256个特征.这些特征用来识别图像里的空间模式，比如线条和物体局部.

全连接层块含3个全连接层。它们的输出个数分别是120、84和10，其中10为输出的类别个数。

net0 = nn.Sequential( nn.Conv2d(1, 6, 5), # in_channels, out_channels, kernel_size nn.Sigmoid(), nn.MaxPool2d(2, 2), # kernel_size, stride nn.Conv2d(6, 16, 5), nn.Sigmoid(), nn.MaxPool2d(2, 2) )batch_size=64X = torch.randn((batch_size,1,28,28))out=net0(X)print(out.shape)

输出

torch.Size([64, 16, 4, 4])

这就是上面我们说的"对我们的输入(28 x 28)来说,卷积层得到的输出shape为[batch,16,4,4]"的由来.

模型定义

至此,我们可以给出LeNet的定义：

class LeNet(nn.Module): def __init__(self): super(LeNet, self).__init__() self.conv = nn.Sequential( nn.Conv2d(1, 6, 5), # in_channels, out_channels, kernel_size nn.Sigmoid(), nn.MaxPool2d(2, 2), # kernel_size, stride nn.Conv2d(6, 16, 5), nn.Sigmoid(), nn.MaxPool2d(2, 2) ) self.fc = nn.Sequential( nn.Linear(16*4*4, 120), nn.Sigmoid(), nn.Linear(120, 84), nn.Sigmoid(), nn.Linear(84, 10) ) def forward(self, img): feature = self.conv(img) output = self.fc(feature.view(img.shape[0], -1)) return output

在forward()中,在输入全连接层之前,要先feature.view(img.shape[0], -1)做一次reshape.

我们用gpu来做训练,所以要把net的参数都存储在显存上:

net = LeNet().cuda()

　数据加载

import torchfrom torch import nnimport syssys.path.append("..") import learntorch_utilsbatch_size,num_workers=64,4train_iter,test_iter = learntorch_utils.load_data(batch_size,num_workers)

load_data定义于learntorch_utils.py,如下:

def load_data(batch_size,num_workers): mnist_train = torchvision.datasets.FashionMNIST(root='/home/sc/disk/keepgoing/learn_pytorch/Datasets/FashionMNIST', train=True, download=True, transform=transforms.ToTensor()) mnist_test = torchvision.datasets.FashionMNIST(root='/home/sc/disk/keepgoing/learn_pytorch/Datasets/FashionMNIST', train=False, download=True, transform=transforms.ToTensor()) train_iter = torch.utils.data.DataLoader( mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers) test_iter = torch.utils.data.DataLoader( mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers) return train_iter,test_iter

定义损失函数

l = nn.CrossEntropyLoss()

定义优化器

opt = torch.optim.Adam(net.parameters(),lr=0.01)

定义评估函数

def test(): acc_sum = 0 batch = 0 for X,y in test_iter: X,y = X.cuda(),y.cuda() y_hat = net(X) acc_sum += (y_hat.argmax(dim=1) == y).float().sum().item() batch += 1 print('acc:%f' % (acc_sum/(batch*batch_size)))

训练

• 前向传播
• 计算loss
• 梯度清空,反向传播
• 更新参数

num_epochs=5def train(): for epoch in range(num_epochs): train_l_sum,batch=0,0 for X,y in train_iter: X,y = X.cuda(),y.cuda() #把tensor放到显存 y_hat = net(X) #前向传播 loss = l(y_hat,y) #计算loss,nn.CrossEntropyLoss中会有softmax的操作 opt.zero_grad()#梯度清空 loss.backward()#反向传播,求出梯度 opt.step()#根据梯度,更新参数 train_l_sum += loss.item() batch += 1 print('epoch %d,train_loss %f' % (epoch + 1,train_l_sum/(batch*batch_size))) test()

输出如下:

epoch 1,train_loss 0.011750acc:0.799064epoch 2,train_loss 0.006442acc:0.855195epoch 3,train_loss 0.005401acc:0.857584epoch 4,train_loss 0.004946acc:0.874602epoch 5,train_loss 0.004631acc:0.874403