网络结构： 对象： 节点，端点 （nodes, vertices） N 交互：链接，边 （links，edges） E 系统：网络，图，图谱 （network，graph） G（N,E) Graph与Network的区别： Network：真实存在的系统，如网络Web，社交网络social network，新陈代谢网络Metabolic network（常用词：network, node, link） Graph: 网络的数学表示，如网络图谱Web graph,社交图谱 Social graph,知识图谱 Knowledge Graph
（常用词：Graph, vertex, edge）
在课程中，会恰当的区分与使用该两个词，但是，大多数情况，将两个词看成是相等的
给每个网络系统选定恰当的词用以表示其实际意义
图的相关术语：
图分类： 无向图：如合作关系，好友关系 有向图：如打电话，twitter的follow 度：节点的边数 平均度：网络的平均度 有向图中区分出度与入度
完全图complete graph：任意两节点相连， 平均度为N-1 二分图Bipartite graph：设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图 例子： 作者——论文 演员——电影 观众/用户——电影 （观看或投票） 菜谱——材料 “folded” networks：作者合作网络，电影协助投票网络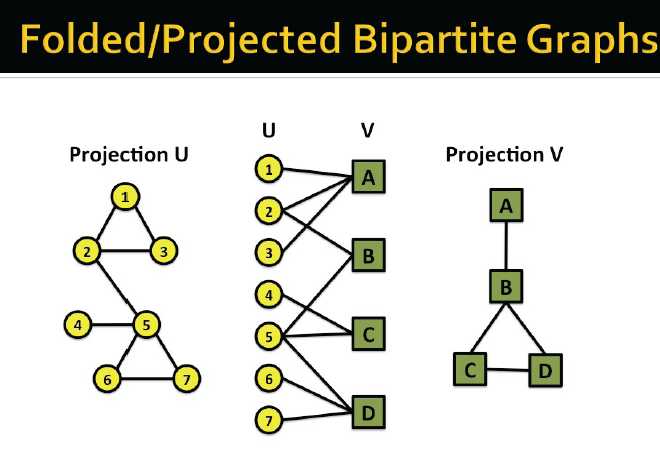
图的表示： 邻接矩阵：有向，无向，稀疏性 set （v1，v2）：更适用于大网络与稀疏网络，可快速查询节点的邻居 显示世界中的很多网络都是稀疏的 边的属性： 权重：如社交的频繁度 排序：如最好的朋友，第二好的朋友 类型：如朋友，亲戚，同事 标签：如信任/不信任，朋友/敌人 连通图：任意两节点间存在直接或间接的链路关系 Bridge edge: If we erase the edge, the graph becomes disconnected Articulation node: If we erase the node, the graph becomes disconnected 强连接有向图：has a path from each node to every other node
and vice versa 弱连接有向图：is connected if we disregard the edge directions 强连通分量Strongly connected components (SCCs) can
be identified, but not every node is part of a nontrivial strongly connected component.
