There are n computers numbered from 0 to n-1 connected by ethernet cables connections forming a network where connections[i] = [a, b] represents a connection between computers a and b. Any computer can reach any other computer directly or indirectly through the network.
Given an initial computer network connections. You can extract certain cables between two directly connected computers, and place them between any pair of disconnected computers to make them directly connected. Return the minimum number of times you need to do this in order to make all the computers connected. If it‘s not possible, return -1.
Example 1:
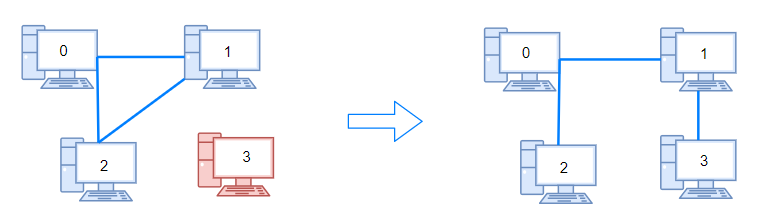
Input: n = 4, connections = [[0,1],[0,2],[1,2]]Output: 1Explanation: Remove cable between computer 1 and 2 and place between computers 1 and 3.
Example 2:
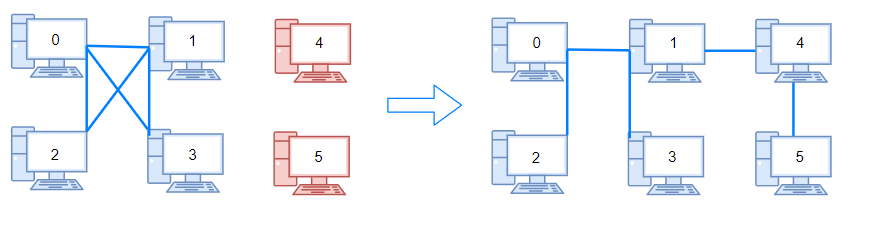
Input: n = 6, connections = [[0,1],[0,2],[0,3],[1,2],[1,3]]Output: 2
Example 3:
Input: n = 6, connections = [[0,1],[0,2],[0,3],[1,2]]Output: -1Explanation: There are not enough cables.
Example 4:
Input: n = 5, connections = [[0,1],[0,2],[3,4],[2,3]]Output: 0
Constraints:
1 <= n <= 10^51 <= connections.length <= min(n*(n-1)/2, 10^5)connections[i].length == 20 <= connections[i][0], connections[i][1] < nconnections[i][0] != connections[i][1]题目意思是给一堆computer和cables,把他们联通需要的最小拆补cable的数量是多少。
第一次遇到用union find做的题目,一时间难以下手。
union find是一种特殊的data structure,用来解决检测是否联通之类的问题,包括了两个主要的method
https://zxi.mytechroad.com/blog/?s=union+find
1. find()
此method是找index为i的节点的祖先,实现的方法有多种,下面的是recursive的一种
private int findParent(int[] par, int i) { if(par[i] == i) return i; return par[i] = findParent(par, par[i]); }
2. merge()
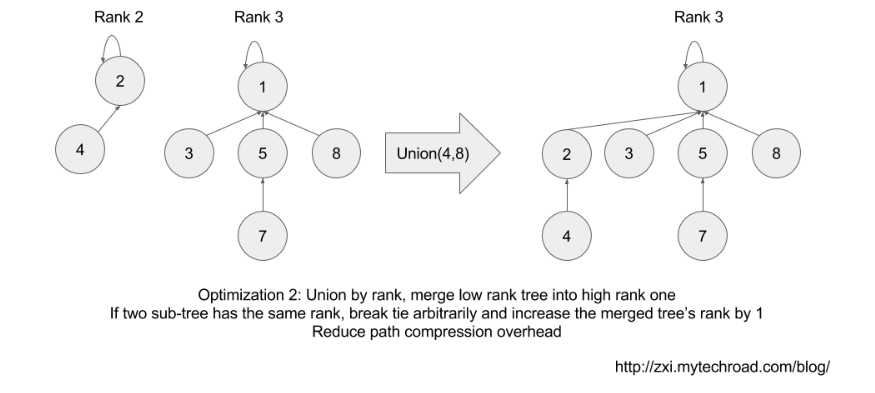
此method是将两个子cluster合并,一般情况是有rank的合并,rank低的合并到rank高的
public boolean Union(int u, int v) { int pu = Find(u); int pv = Find(v); if (pu == pv) return false; if (ranks_[pv] > ranks_[pu]) parents_[pu] = pv; else if (ranks_[pu] > ranks_[pv]) parents_[pv] = pu; else { parents_[pv] = pu; ranks_[pu] += 1; } return true; }
回到我们的题上,首先应该注意到,如果cable数<电脑数-1的话无论如何都不可能成功,
否则直接连通分量的数量components-1就是要求的最小值。
class Solution { public int makeConnected(int n, int[][] connections) { if (connections.length < n - 1) return -1; // To connect all nodes need at least n-1 edges int[] parent = new int[n]; for (int i = 0; i < n; i++) parent[i] = i; int components = 0; for (int[] connection : connections) { int p1 = findParent(parent, connection[0]); int p2 = findParent(parent, connection[1]); parent[p2] = p1;//小(p2)merge到大(parent【p2】=p1) System.out.println("p1:" + p1 + ", p2:" + p2); } for (int i = 0; i < n; i++) if (parent[i] == i) { components++; System.out.println("parent["+i+"]:"+parent[i]); } return components - 1; // Need (components-1) cables to connect components together } private int findParent(int[] par, int i) { if(par[i] == i) return i; return par[i] = findParent(par, par[i]); }}
先findparent,find的同时更新parent,因为rank一样所以可以merge到任何一边,
merge完后计算一共有多少个components联通分量,减一就是结果了。
也可以用dfs
花花酱:https://www.youtube.com/watch?v=8d8vfU3LYHM
union find的其他references:
https://www.jianshu.com/p/def7767982ac
https://blog.csdn.net/guoziqing506/article/details/78752557
https://www.cnblogs.com/zmyvszk/p/5351494.html
https://segmentfault.com/a/1190000012898131