1、AlexNet 模型简介
由于受到计算机性能的影响,虽然LeNet在图像分类中取得了较好的成绩,但是并没有引起很多的关注。 知道2012年,Alex等人提出的AlexNet网络在ImageNet大赛上以远超第二名的成绩夺冠,卷积神经网络乃至深度学习重新引起了广泛的关注。
2、AlexNet 模型特点
AlexNet是在LeNet的基础上加深了网络的结构,学习更丰富更高维的图像特征。AlexNet的特点:
1)更深的网络结构
2)使用层叠的卷积层,即卷积层+卷积层+池化层来提取图像的特征
3)使用Dropout抑制过拟合
4)使用数据增强Data Augmentation抑制过拟合
5)使用Relu替换之前的sigmoid的作为激活函数
6)多GPU训练
ReLu作为激活函数
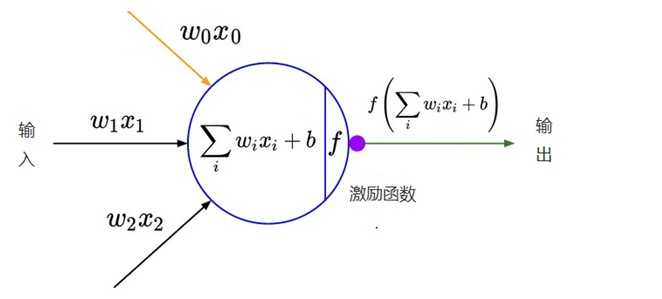
在最初的感知机模型中,输入和输出的关系如下:
${y = \sum\limits_i {{w_i}{x_i}} + b}$
只是单纯的线性关系,这样的网络结构有很大的局限性:即使用很多这样结构的网络层叠加,其输出和输入仍然是线性关系,无法处理有非线性关系的输入输出。因此,对每个神经元的输出做个非线性的转换也就是,将上面就加权求和${\sum\nolimits_i {{w_i}{x_i}} + b}$的结果输入到一个非线性函数,也就是激活函数中。 这样,由于激活函数的引入,多个网络层的叠加就不再是单纯的线性变换,而是具有更强的表现能力。
在最初,sigmoid和tanh函数最常用的激活函数。
1) sigmoid
${\sigma \left( x \right) = \frac{1}{{1 + {e^{ - x}}}}}$
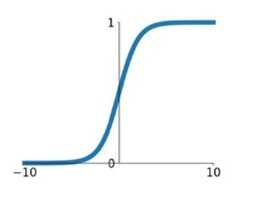
在网络层数较少时,sigmoid函数的特性能够很好的满足激活函数的作用:它把一个实数压缩至0到1之间,当输入的数字非常大的时候,结果会接近1;当输入非常大的负数时,则会得到接近0的结果。这种特性,能够很好的模拟神经元在受刺激后,是否被激活向后传递信息(输出为0,几乎不被激活;输出为1,完全被激活)。
sigmoid一个很大的问题就是梯度饱和。 观察sigmoid函数的曲线,当输入的数字较大(或较小)时,其函数值趋于不变,其导数变的非常的小。这样,在层数很多的的网络结构中,进行反向传播时,由于很多个很小的sigmoid导数累成,导致其结果趋于0,权值更新较慢。
2) ReLu
${ReLU\left( x \right) = max\left( {0\user1{,}x} \right)}$
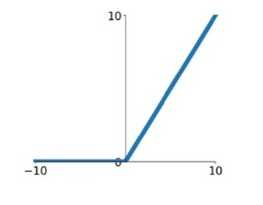
针对sigmoid梯度饱和导致训练收敛慢的问题,在AlexNet中引入了ReLU。ReLU是一个分段线性函数,小于等于0则输出为0;大于0的则恒等输出。相比于sigmoid,ReLU有以下有点:
1)计算开销下。sigmoid的正向传播有指数运算,倒数运算,而ReLu是线性输出;反向传播中,sigmoid有指数运算,而ReLU有输出的部分,导数始终为1.
2)梯度饱和问题
3)稀疏性。Relu会使一部分神经元的输出为0,这样就造成了网络的稀疏性,并且减少了参数的相互依存关系,缓解了过拟合问题的发生。
这里有个问题,前面提到,激活函数要用非线性的,是为了使网络结构有更强的表达的能力。那这里使用ReLU本质上却是个线性的分段函数,是怎么进行非线性变换的。 这里把神经网络看着一个巨大的变换矩阵M,其输入为所有训练样本组成的矩阵A,输出为矩阵B。
${B = M \cdot A}$
这里的M是一个线性变换的话,则所有的训练样本A进行了线性变换输出为B。 那么对于ReLU来说,由于其是分段的,0的部分可以看着神经元没有激活,不同的神经元激活或者不激活,其神经玩过组成的变换矩阵是不一样的。也就是说,每个训练样本使用的线性变换矩阵是不一样的,在整个训练样本空间来说,其经历的是非线性变换。
简单来说,不同训练样本中的同样的特征,在经过神经网络学习时,流经的神经元是不一样的(激活函数值为0的神经元不会被激活)。这样,最终的输出实际上是输入样本的非线性变换。单个训练样本是线性变换,但是每个训练样本的线性变换是不一样的,这样整个训练样本集来说,就是非线性的变换。
数据增强
神经网络由于训练的参数多,表能能力强,所以需要比较多的数据量,不然很容易过拟合。当训练数据有限时,可以通过一些变换从已有的训练数据集中生成一些新的数据,以快速地扩充训练数据。对于图像数据集来说,可以对图像进行一些形变操作:
1) 翻转
2) 随机裁剪
3)平移,颜色光照的变换
...
AlexNet中对数据做了以下操作:
1)随机裁剪,对256×256的图片进行随机裁剪到227×227,然后进行水平翻转。
2)测试的时候,对左上、右上、左下、右下、中间分别做了5次裁剪,然后翻转,共10个裁剪,之后对结果求平均。
3)对RGB空间做PCA(主成分分析),然后对主成分做一个(0, 0.1)的高斯扰动,也就是对颜色、光照作变换,结果使错误率又下降了1%。
层叠池化
在LeNet中池化是不重叠的,即池化的窗口的大小和步长是相等的,如下:
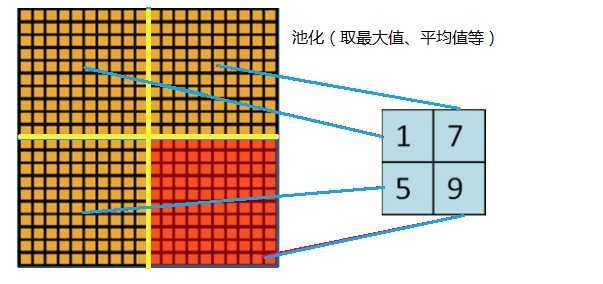
在AlexNet中使用的池化(Pooling)却是可重叠的,也就是说,在池化的时候,每次移动的步长小于池化的窗口长度。AlexNet池化的大小为3×3的正方形,每次池化移动步长为2,这样就会出现重叠。重叠池化可以避免过拟合,这个策略贡献了0.3%的Top-5错误率。与非重叠方案s=2,z=2相比,输出的维度是相等的,并且能在一定程度上抑制过拟合。
局部相应归一化
ReLU具有让人满意的特性,它不需要通过输入归一化来防止饱和。如果至少一些训练样本对ReLU产生了正输入,那么那个神经元上将发生学习。然而,我们仍然发现接下来的局部响应归一化有助于泛化。${a_{x{,}y}^i}$表示神经元激活,通过在(x,y)(位置应用核${i}$然后应用ReLU非线性来计算,响应归一化激活${b_{x{,}y}^i}$通过下式给定:
${b_{x{,}y}^i = \frac{{a_{x{,}y}^i}}{{{{\left( {k + \alpha \sum\limits_{j = {max}\left( {{0,}{{{i - n}} \mathord{\left/
{\vphantom {{{i - n}} 2}} \right.
\kern-\nulldelimiterspace} 2}} \right)}^{{min(N - 1,}{{{i + n}} \mathord{\left/
{\vphantom {{{i + n}} 2}} \right.
\kern-\nulldelimiterspace} 2}{)}} {{{\left( {a_{x{,}y}^j} \right)}^2}} } \right)}^\beta }}}}$
其中,N是卷积核的个数,也就是生成的FeatureMap的个数;${k{,}\alpha {,}\beta {,}n}$是超参数,论文中使用的值是${k = 2{,}\alpha = {10^{ - 4}}{,}\beta = 0.75{,}n = 5}$。输出${b_{x{,}y}^i}$和输入${a_{x{,}y}^i}$的上标表示的是当前值所在的通道,也即是叠加的方向是沿着通道进行。将要归一化的值${a_{x{,}y}^i}$所在附近通道相同位置的值的平方累加起来${\sum\nolimits_{j = {max}\left( {{0,}{{{i - n}} \mathord{\left/
{\vphantom {{{i - n}} 2}} \right.
\kern-\nulldelimiterspace} 2}} \right)}^{{min(N - 1,}{{{i + n}} \mathord{\left/
{\vphantom {{{i + n}} 2}} \right.
\kern-\nulldelimiterspace} 2}{)}} {{{\left( {a_{x{,}y}^j} \right)}^2}} }$
Dropout
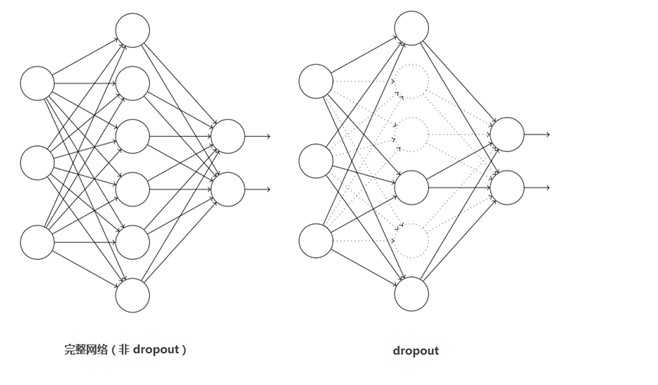
这个是比较常用的抑制过拟合的方法了。 引入Dropout主要是为了防止过拟合。在神经网络中Dropout通过修改神经网络本身结构来实现,对于某一层的神经元,通过定义的概率将神经元置为0,这个神经元就不参与前向和后向传播,就如同在网络中被删除了一样,同时保持输入层与输出层神经元的个数不变,然后按照神经网络的学习方法进行参数更新。在下一次迭代中,又重新随机删除一些神经元(置为0),直至训练结束。 Dropout应该算是AlexNet中一个很大的创新,现在神经网络中的必备结构之一。Dropout也可以看成是一种模型组合,每次生成的网络结构都不一样,通过组合多个模型的方式能够有效地减少过拟合,Dropout只需要两倍的训练时间即可实现模型组合(类似取平均)的效果,非常高效。 如下图:
3、Alex网络结构
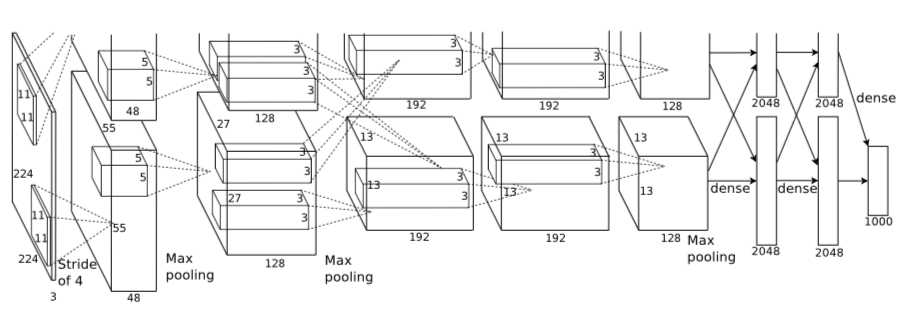
注:上图中的输入是224×224,不过经过计算(224−11)/4=54.75并不是论文中的55×55,而使用227×227作为输入,则(227−11)/4=55。
网络包含8个带权重的层;前5层是卷积层,剩下的3层是全连接层。最后一层全连接层的输出是1000维softmax的输入,softmax会产生1000类标签的分布网络包含8个带权重的层;前5层是卷积层,剩下的3层是全连接层。最后一层全连接层的输出是1000维softmax的输入,softmax会产生1000类标签的分布。
该层的处理流程是: 卷积-->ReLU-->池化-->归一化。
1)卷积,输入是227×227,使用96个11×11×3的卷积核,得到的FeatureMap为55×55×96。
2)ReLU,将卷积层输出的FeatureMap输入到ReLU函数中。
3)池化,使用3×3步长为2的池化单元(重叠池化,步长小于池化单元的宽度),输出为27×27×96((55−3)/2+1=27)。
4)局部响应归一化,使用k=2,n=5,α=10−4,β=0.75进行局部归一化,输出的仍然为27×27×96,输出分为两组,每组的大小为27×27×48。
该层的处理流程是:卷积-->ReLU-->池化-->归一化。
1)卷积,输入是2组27×27×48。使用2组,每组128个尺寸为5×5×48的卷积核,并作了边缘填充padding=2,卷积的步长为1. 则输出的FeatureMap为2组,每组的大小为 27×27 times128. ((27+2∗2−5)/1+1=27)。
2)ReLU,将卷积层输出的FeatureMap输入到ReLU函数中。
3)池化运算的尺寸为3×3,步长为2,池化后图像的尺寸为(27−3)/2+1=13,输出为13×13×256。
4)局部响应归一化,使用k=2,n=5,α=10−4,β=0.75进行局部归一化,输出的仍然为13×13×256,输出分为2组,每组的大小为13×13×128。
该层的处理流程是: 卷积-->ReLU。
1)卷积,输入是13×13×256,使用2组共384尺寸为3×3×256的卷积核,做了边缘填充padding=1,卷积的步长为1.则输出的FeatureMap为13×13 times384。
2)ReLU,将卷积层输出的FeatureMap输入到ReLU函数中。
该层的处理流程是: 卷积-->ReLU
该层和C3类似。
1)卷积,输入是13×13×384,分为两组,每组为13×13×192.使用2组,每组192个尺寸为3×3×192的卷积核,做了边缘填充padding=1,卷积的步长为1.则输出的FeatureMap为13×13 times384,分为两组,每组为13×13×192。
2)ReLU,将卷积层输出的FeatureMap输入到ReLU函数中。