一。配置Nginx隐藏版本号

在生产环境中，需要隐藏Nginx的版本号，以避免安全漏洞的泄露

需要记住三个命令

1.    elinks –dump 本机IP

2.       curl -I 本机IP

3.       lynx 本机IP

查看ngxin版本及型号

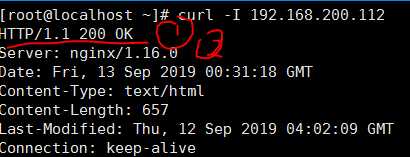
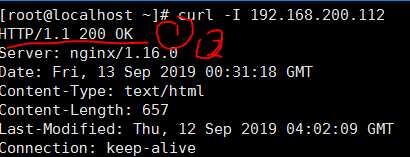
二。修改Nginx用户与组

三。配置Nginx网页缓存时间

四。配置Nginx实现连接超时

五。更改Nginx运行进程数

六。配置Nginx实现网页压缩功能

七。配置Nginx实现防盗链功能

八

在生产环境中，需要隐藏Nginx的版本号，以避免安全漏洞的泄露