预编译的两种情况
全局:
1.全局 直接是script标签中的代码,不包括函数执行
执行前:
1.首先生成一个GO(global object)对象,看不到,但是可以模拟出来用来分析
2.分析变量声明,变量名为属性名,值为undefined
3.分析函数声明,函数名为属性名,值为函数体,如果函数名和变量名相同,则无情覆盖
函数内部:
1.函数调用,也是会生成自己的作用域(AO:active object),AO活动对象. 函数调用时候,执行前的一瞬间产生的,如果有多个函数的调用,会产生多个AO
1.1 函数执行前的一瞬间,生成AO活动对象
1.2 分析参数,形参作为对象的属性名,实参作为对象的属性值
1.3 分析变量声明,变量名为属性名,值为undefined,如果遇到AO对象上属性同名,不去做任何改变
1.4 分析<b>函数声明</b>,函数名为属性名,值为函数体,如果遇到AO对象上属性同名,则无情覆盖
2.逐行执行
举例时间:
简单版本-全局:
<script type="text/javascript">
console.log(a);//a函数函数体
var a=10;
function a(){
}
</script>
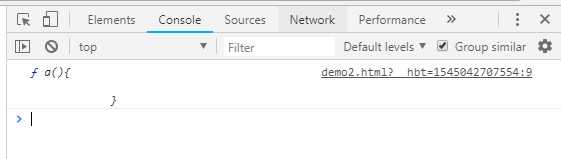
1.首先生成一个GO(global object)对象,看不到,但是可以模拟出来用来分析
GO{
}
2.分析变量声明,变量名为属性名,值为undefined
GO{
a:underfined
}
3.分析函数声明,函数名为属性名,值为函数体,如果函数名和变量名相同,则无情覆盖
GO{
a:function a(){
}
}
简单版本-局部1:
<script type="text/javascript"> function fun(test){ console.log(test);//5 var test = 10; console.log(test);//10 } fun(5);</script>

1.函数执行前的一瞬间,生成AO活动对象
AO{
}
2.分析参数,形参作为对象的属性名,实参作为对象的属性值
AO{
test:5;
}
3. 分析变量声明,变量名为属性名,值为undefined,如果遇到AO对象上属性同名,不去做任何改变
AO{
test:5;
}
简单版本-局部2:
<script type="text/javascript"> function fun(test){ console.log(test);//test函数体 var test = 10;//给test赋值为10 function test(){//声明函数 } console.log(test);//10 } fun(5);</script>
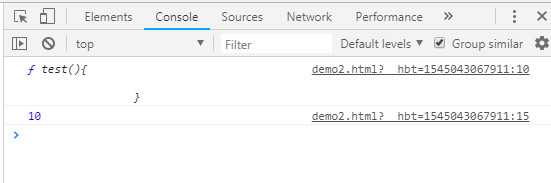
1.函数执行前的一瞬间,生成AO活动对象
AO{
}
2.分析参数,形参作为对象的属性名,实参作为对象的属性值
AO{
test:5;
}
3. 分析变量声明,变量名为属性名,值为undefined,如果遇到AO对象上属性同名,不去做任何改变
AO{
test:5;
}
4. 分析<b>函数声明</b>,函数名为属性名,值为函数体,如果遇到AO对象上属性同名,则无情覆盖
AO{
test:function(){};
}
5.逐行执行
然后开始一行一行执行代码,第一个console.log输出的结果是test的函数体
下一行就是给test赋值为5,
下一行就是函数体的声明,不做处理
下一行就是console.log输出的结果就是10
复杂版本:
1 <script type="text/javascript"> 2 console.log(test); 3 function test(test){ 4 console.log(test); 5 var test = 123; 6 console.log(test); 7 function test(){ 8 9 }10 console.log(test);11 var test = function(){}12 console.log(test);13 }14 test(10);15 var test = 45616 console.log(test);17 </script>
预编译开始,先生成一个GO{
}
1.看变量GO{
test:underfined
}
2.看函数声明GO{
test:function test(test){
console.log(test);
var test = 123;
console.log(test);
function test(){
}
console.log(test);
var test = function(){}
console.log(test);
}
}
把整个函数体给test
预编译完成,开始执行代码,第二行的结果是test函数的函数体
3到13行都是函数声明,不用管
第14行函数执行,传入参数10
函数执行的时候产生AO{
}
1.看参数AO{
test:10
}
2.看变量,变量同名,不用管变量AO{
test:10
}
3.看函数,函数和参数同名,函数把参数覆盖AO{
test:function test(){}
}
4.逐行执行
第三行打印名字为test的函数体,
第四行给test赋值123,第五行打印123
7到9行函数体声明不用管
第十行打印123
第十一行把一个匿名函数(没有函数名的函数)赋值给test
第十二行函数执行完毕
第十四行回到全局,把456赋值给test
第十五行打印456